
Решение линейных уравнений – это одно из базовых умений, которое необходимо освоить в школе. Однако, не всем ученикам удаётся полностью понять и уверенно решать такие уравнения с первого раза. Если ты часто сталкиваешься с трудностями в этой области, то эта статья специально для тебя!
Мы рассмотрим метод решения линейных уравнений, который называется методом Крамера. Он основан на использовании матрицы коэффициентов и определителя этой матрицы. В общем виде, уравнение можно записать как Ax = b, где A – матрица коэффициентов, x – вектор неизвестных, b – вектор свободных членов. Если определитель матрицы A не равен нулю, то система имеет единственное решение.
Метод Крамера заключается в последовательном вычислении определителей матриц, полученных из матрицы коэффициентов путём замены соответствующего столбца на вектор свободных членов. Процесс повторяется для каждой неизвестной переменной, и в итоге получается система уравнений, решение которой состоит из отношений определителей к определителю основной матрицы A.
Вы можете найти курсы огэ по математике в онлайн школе Skysmart!
Удивительно, что метод Крамера позволяет решать любые системы линейных уравнений без необходимости применения сложных формул и почленного расчёта. Этот «школьный» метод позволяет найти верное решение с минимальными усилиями, используя лишь базовые понятия из области линейной алгебры.
Как понять и решить линейные уравнения одним разом
Метод Крамера
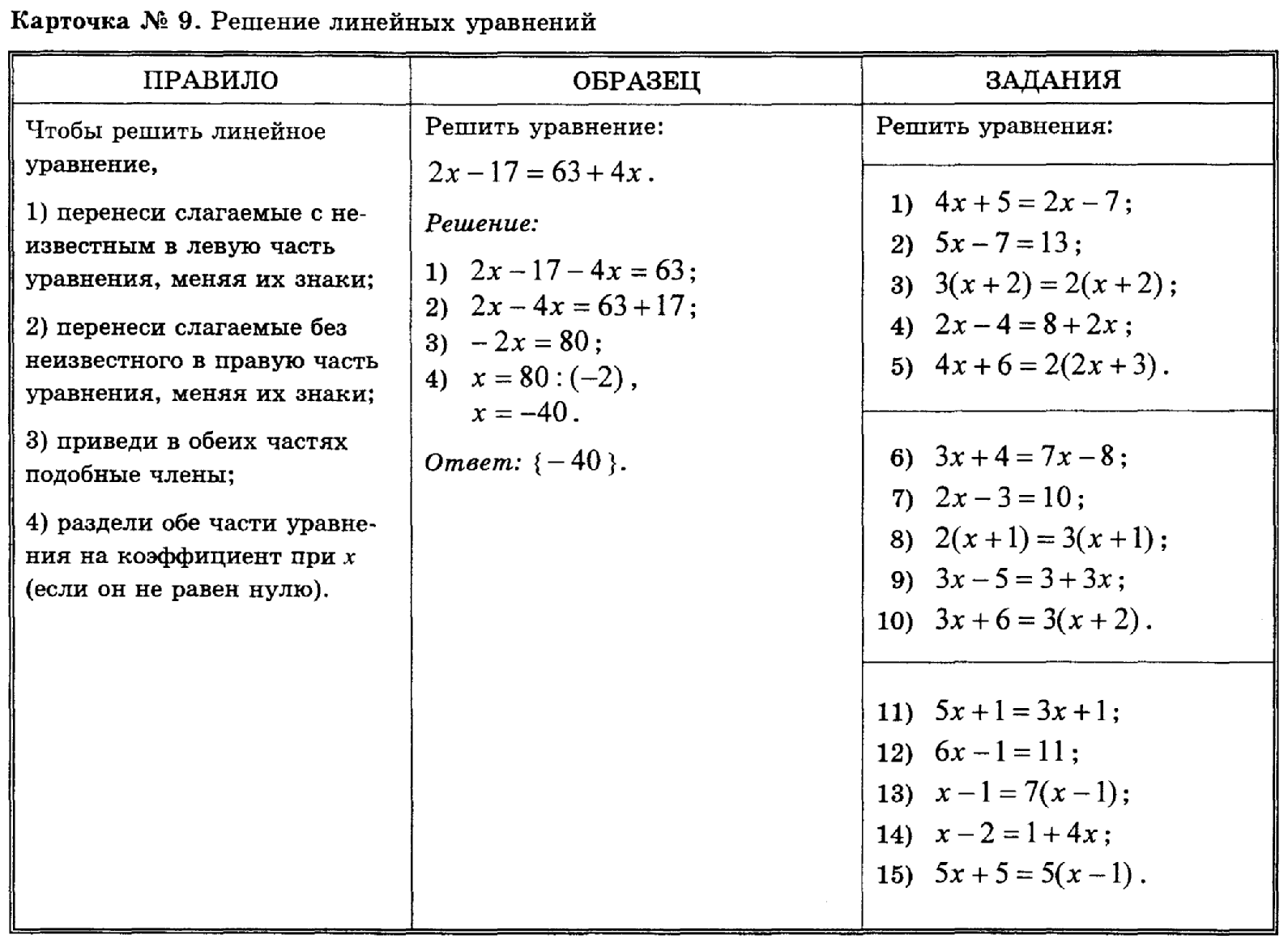
Основная идея метода Крамера состоит в решении системы линейных уравнений с помощью определителей. Рассмотрим систему уравнений вида:
x1 + a1 x2 + … + a1n-1 xn = b1
..
..
..
an-1 x2 + x1 + an-1n-1 xn = bn-1
an x2 + an x1 + …. + xn = bn
Чтобы решить эту систему, сначала запишем коэффициенты при неизвестных в виде матрицы:
| 1 a1 a1n-1 … b1 |
| .. .. .. .. .. |
| .. .. .. .. .. |
| .. .. .. .. .. |
| an-1 1 an-1n-1 … bn-1 |
| an an … … 1 bn |
Затем, находим определитель этой матрицы. Если определитель равен нулю, то система уравнений не имеет решений. Если определитель не равен нулю, то система имеет единственное решение.
Далее, чтобы найти значения неизвестных, мы последовательно заменяем столбцы свободных членов в исходной матрице на столбцы коэффициентов неизвестных, а затем находим определитель каждой из полученных матриц. Определитель каждой из этих матриц делим на определитель основной матрицы. Полученные значения подставляем в исходную систему уравнений и убеждаемся, что получается верное равенство.
Таким образом, используя метод Крамера, можно понять и решить линейные уравнения одним разом.
Математическая основа линейных уравнений
Основным инструментом для решения линейных уравнений является система уравнений. Система линейных уравнений представляет собой набор уравнений, заданных относительно одних и тех же переменных.
Систему уравнений можно записать в матричной форме. Для этого левая часть каждого уравнения записывается в виде матрицы, а переменная – в виде столбца. Умножение матрицы на столбец переменных соответствует вычислению левой части системы уравнений.
Решение системы уравнений осуществляется методом Гаусса. Суть этого метода заключается в последовательном преобразовании уравнений системы с целью выражения переменных через другие переменные.
На первом шаге метода Гаусса выделяют главный элемент – это первое ненулевое число в каждом уравнении, которое находится на главной диагонали матрицы. Далее, путем сложения строк с коэффициентами, пропорциональными главному элементу, достигается обнуление всех остальных чисел под главным элементом методом приведения системы к треугольному виду (или ступенчатому виду).
На следующих шагах метода Гаусса коэффициенты при переменных выполняются лишь с помощью сложения и вычитания. Это позволяет с легкостью получить решение системы уравнений.
В результате последовательных преобразований системы с помощью метода Гаусса получается система с верхней треугольной матрицей. Элементы на главной диагонали матрицы называются главными элементами системы.
Обратная подстановка – это способ построения решения системы уравнений с верхней треугольной матрицей. Суть данного метода заключается в поочередном подставлении найденных ранее значений переменных в уравнения, начиная с последнего и двигаясь вверх до первого уравнения системы. Подстановка позволяет найти значения всех переменных.
Таким образом, решая линейные уравнения с помощью метода Гаусса и обратной подстановки, можно полностью понять и решить систему уравнений за один раз.
Школьный метод решения системы линейных уравнений с двумя переменными
Систему линейных уравнений с двумя переменными можно решить и с помощью «школьного метода». Для этого сначала одно из уравнений записываем в виде y = ax + b, а затем подставляем это выражение во второе уравнение. Получается уравнение с одной переменной (обычно x или y), которое легко решается. Затем найденное значение подставляется в первое уравнение, и получается верное равенство. Таким образом, можно найти значения обоих переменных.
Дополнительные сведения о решении линейных уравнений
При решении системы линейных уравнений возможны различные случаи и периодические свойства чисел и выражений. Матрица, составленная из коэффициентов переменных системы уравнений, называется матрицей системы. Ее определитель играет важную роль в анализе системы уравнений.
Линейные уравнения – это одна из основ математики и фундаментальных понятий в области алгебры. Изучая и решая линейные уравнения, ты сможешь успешно решать задачи из разных областей науки и применять полученные знания в реальной жизни.
Объяснение основных понятий линейных уравнений
Алгебраическая система и система уравнений
Система уравнений, состоящая из любых уравнений, называется алгебраической системой. В случае линейных уравнений система называется системой линейных уравнений.
Метод Гаусса
Одним из методов решения систем линейных уравнений является метод Гаусса. Он заключается в пошаговом преобразовании системы с помощью операций над ее уравнениями. В итоге система приводится к эквивалентной системе с верным определением переменных.
Метод Крамера
Метод Крамера позволяет найти решение системы линейных уравнений с помощью вычисления определителей. Коэффициенты при переменных образуют матрицу, а столбец свободных членов – вектор. Затем с помощью определителей находятся значения переменных.
Метод подстановки
Метод подстановки является одним из способов решения линейных уравнений. В первом уравнении системы находится значение одной переменной через другие. Затем найденное значение подставляется во второе уравнение, и так далее. В результате получается решение системы.
Метод поочередного исключения
Метод поочередного исключения – это способ решения системы линейных уравнений путем пошагового вычитания одного уравнения системы из другого. Таким образом, система постепенно сводится к системе с меньшим числом уравнений и переменных. В конечном результате получается система с одним уравнением и одной переменной.
Определение решения системы линейных уравнений
Решение системы линейных уравнений – это такой набор значений переменных, при подстановке которого в каждое уравнение системы получается верное равенство. Если при подстановке получится нулевое значение, то система называется несовместной.
Матрица системы уравнений
Матрица системы уравнений представляет собой таблицу, в которой каждая строка соответствует уравнению, а каждый столбец – переменной. Коэффициенты перед переменными записываются в соответствующих местах матрицы.
| Переменная 1 | Переменная 2 | Переменная 3 | |
|---|---|---|---|
| Уравнение 1 | Коэффициент 11 | Коэффициент 12 | Коэффициент 13 |
| Уравнение 2 | Коэффициент 21 | Коэффициент 22 | Коэффициент 23 |
| Уравнение 3 | Коэффициент 31 | Коэффициент 32 | Коэффициент 33 |
Матрица может быть прямоугольной или квадратной, в зависимости от количества уравнений и переменных в системе.
Теперь, увидев полное объяснение основных понятий линейных уравнений, ты сможешь легче понять и решить любые задачи по данной теме!
Заключение
Линейные уравнения – это основа алгебры и математики в целом. Понимание основных понятий и методов решения линейных уравнений поможет тебе в решении задач и применении их в реальной жизни. Учитель также сможет объяснить тебе эти концепции с помощью данной статьи и помочь в понимании твоих слабых мест в данной теме. Так что не упусти возможность изучить линейные уравнения вместе с нами!
Порядок решения линейных уравнений
Для начала, рассмотрим уравнение вида:
ax + by + cz = d
где a, b, c и d — любые числа.
Метод Гаусса
Один из основных методов решения линейных уравнений — метод Гаусса, также называемый «школьный метод».
Для его применения, необходимо представить систему уравнений в виде матрицы. Первая строка матрицы представляет уравнение вида ax + by + cz = d, где каждый коэффициент a, b и c находится в отдельном столбце, а константа d находится в самом правом столбце.
Далее, необходимо привести матрицу к треугольному виду с помощью элементарных преобразований. Элементарные преобразования могут быть следующими: сложение или вычитание строк, умножение строки на число и перестановка строк местами.
Поочередно применяя эти преобразования к каждой строке матрицы, получаем систему уравнений, в которой в каждой следующей строке стоит на одну переменную меньше, а в последней строке остается одно уравнение с одной переменной.
Далее, начиная с последней строки и двигаясь вверх, находим значения переменных путем обратной подстановки. Значение последней переменной сразу получаем, так как в последнем уравнении у нас осталась только одна переменная. Далее, подставляем полученное значение в предыдущее уравнение и находим значение предпоследней переменной и так далее, пока не найдем значения всех переменных.
Метод Крамера
Еще один метод решения линейных уравнений — метод Крамера, который основан на определителях и минорах матрицы системы уравнений.
Для применения этого метода, система уравнений должна иметь одинаковое количество уравнений и неизвестных.
Матрица системы уравнений представляет собой квадратную матрицу размерности n x n, где n — количество переменных в системе. В данном случае, каждая строка матрицы соответствует одному уравнению, а столбец — соответствует одной переменной.
Определить методом Крамера можно, имеет ли система уравнений решение или нет. Если определитель матрицы системы уравнений равен нулю, то система уравнений не имеет решения.
Если определитель не равен нулю, то можно найти значения каждой переменной, используя определители и миноры матрицы.
Определители и миноры матрицы находятся путем вычеркивания одной строки и одного столбца из матрицы. Затем определитель находится для полученной минорной матрицы.
Значение каждой переменной находится путем деления определителя соответствующего минора на определитель матрицы системы уравнений.
В итоге, получаем значения всех переменных и тем самым находим решение системы уравнений.
Заключение
Понимание и решение линейных уравнений является важной частью математики и может быть полностью освоено при использовании методов Гаусса и Крамера.
Необходимо понимать, что в обоих методах уравнения решаются поочередно, одно за другим, шаг за шагом. Важно внимательно следить за каждым шагом решения и правильно применять элементарные преобразования и определители матрицы.
При этом, следует помнить, что решение системы уравнений может быть единственным и определенным, а также может быть бесконечным и зависеть от свободных переменных.
Однако, с помощью методов Гаусса и Крамера, любая система линейных уравнений может быть решена конечным числом шагов, и решение всегда может быть найдено.
Теперь ты можешь увидеть, что решение линейных уравнений не так уж и сложно, и у тебя появился новый инструмент — матрица, который поможет тебе в решении подобных задач.
Методы решения линейных уравнений
В данной статье мы рассмотрим несколько основных методов решения линейных уравнений.
1. Метод Гаусса. Данный метод основан на приведении системы уравнений к треугольному виду при помощи элементарных преобразований строк матрицы системы. Суть метода Гаусса заключается в следующем:
- Записываем систему уравнений в матричной форме.
- Приводим матрицу системы к треугольному виду при помощи элементарных преобразований: вычитания двух строк, умножения строки на ненулевое число и перестановки строк местами.
- Получаем систему из n уравнений с n неизвестными.
- Решаем полученную систему методом обратной подстановки.
2. Метод Крамера. Данный метод основан на использовании определителей матрицы системы уравнений. Суть метода Крамера заключается в следующем:
- Записываем систему уравнений в матричной форме.
- Вычисляем главный определитель матрицы системы.
- Вычисляем определители матриц систем, полученных заменой столбцов главной матрицы на столбцы свободных членов.
- Делим значения определителей на главный определитель и находим значения неизвестных.
Оба метода позволяют найти решение системы линейных уравнений, однако у метода Крамера есть некоторые особенности. В случае, когда главный определитель равен нулю, система может не иметь решения или иметь бесконечное количество решений. Также, метод Крамера требует вычисления определителей, что может быть очень трудоемким при большом количестве переменных.
Особенности решения системы линейных уравнений
Для решения системы линейных уравнений необходимо найти такие значения переменных, при которых все уравнения системы будут выполняться. Это называется нахождением решения системы уравнений.
Одним из способов решения системы линейных уравнений является метод Гаусса. Суть этого метода заключается в поэтапных операциях над строками и столбцами матрицы системы уравнений, приводящих ее к эквивалентной матрице, где в главном столбце есть единственный ненулевой элемент. В таком случае легко получить решение системы.
Для начала приведем систему к матричному виду, представив коэффициенты перед переменными в системе уравнений в виде матрицы. Система уравнений:
1. Уравнение 1: a₁₁x₁ + a₁₂x₂ + … + a₁nxₙ = b₁
2. Уравнение 2: a₂₁x₁ + a₂₂x₂ + … + a₂nxₙ = b₂
…
n. Уравнение n: aₙ₁x₁ + aₙ₂x₂ + … + aₙnxₙ = bₙ
Можно записать в виде:
AX = B
где:
A — матрица коэффициентов,
X — матрица значений переменных,
B — матрица свободных членов.
Далее применяются операции над строками матрицы А для приведения ее к ступенчатому виду. В итоге, если система имеет решение, в последней строке матрицы А остаются ненулевые элементы, а в столбце B — значения свободных членов.
Затем применяются обратные операции по строкам для приведения матрицы к единичному виду. Полученная матрица X является решением системы уравнений.
Один из вариантов метода Гаусса — метод обратной матрицы. В этом случае находим обратную матрицу A⁻¹ и осуществляем умножение справа на матрицу B:
X = A⁻¹ * B
Итак, для решения системы линейных уравнений следует использовать различные методы, такие как метод Крамера, метод Гаусса и метод подстановки. Каждый из этих методов позволяет найти решение системы уравнений, опираясь на линейные алгебраические операции.
Метод Крамера
Метод Крамера основан на определении дополнительных матриц, называемых минорами, и определителя матрицы A. Для нахождения решения системы линейных уравнений по методу Крамера необходимо выполнить следующие шаги:
- Вычислить определитель матрицы A.
- Для каждой переменной xᵢ вычислить определитель Dᵢ, в котором i-й столбец матрицы A заменен на столбец свободных членов B.
- Решением системы уравнений будет вектор X, состоящий из значений x₁, …, xₙ, где xᵢ = Dᵢ / D.
Метод подстановки
Метод подстановки подразумевает последовательное выражение переменных в системе уравнений одна за другой. Например, решим систему:
- Уравнение 1: 3x + 2y = 7
- Уравнение 2: 4x — y = -3
Выберем первое уравнение и выразим x:
x = (7 — 2y) / 3
Подставим это значение x во второе уравнение:
4((7 — 2y) / 3) — y = -3
После вычислений найдем значение y:
y = 2
Теперь воспользуемся найденным значением y и найдем значение x по первому уравнению:
x = (7 — 2(2)) / 3 = 1
Таким образом, решение системы уравнений будет x = 1, y = 2.
Заключение
Решение системы линейных уравнений может быть достигнуто различными методами, такими как метод Гаусса, метод Крамера и метод подстановки. Выбор метода зависит от конкретной системы и предпочтений решающего.
Решение системы линейных уравнений по формулам Крамера
Данная часть статьи посвящена решению системы линейных уравнений с помощью формул Крамера. Если у нас есть система уравнений вида:
1. Школьный метод
Предположим, что учителем решено решить систему по первой части школьного курса.
1 выбираем одну переменную и извлекаем ее в первом уравнении. Вторую переменную можно найти путем подсчета суммы коэффициентов переменных со слагаемыми обратно в уравнении.
Например, дана следующая система:
2x + 3y = 8
4x — y = -2
Мы записываем коэффициенты переменных и свободный член в виде матрицы:
Матрица левой части:
| 2 3 |
| 4 -1 |
Матрица переменных:
| x |
| y |
Матрица правой части:
| 8 |
| -2 |
Затем, применяя метод сложения и вычитания строк матрицы, необходимо получить матрицу переменных:
| 1 1 |
| 4 -1 |
Далее, решаем уравнение методом подстановки и увидев решение вида (x, y), подставляем в матрицу переменных и находим верные значения переменных.
2. Метод Крамера
Метод Крамера — это еще один способ нахождения решений систем линейных уравнений. В данном случае, систему уравнений можно записать в виде матричного уравнения Ax = b, где А — матрица коэффициентов системы, x — матрица переменных, b — столбец свободных членов.
Для решения системы методом Крамера, необходимо находить значение каждой переменной как отношение определителей матриц A и b к определителю матрицы A. То есть, решение системы будет иметь вид:
x = |Ax| / |A|
y = |Ay| / |A|
где |Ax|, |Ay| — определители, где вместо столбца переменной x и y стоит столбец свободных членов b.
Таким образом, для данной системы уравнений:
2x + 3y = 8
4x — y = -2
Мы записываем коэффициенты переменных и свободный член в виде матрицы:
| 2 3 |
| 4 -1 |
Так как у нас две переменные (x и y), то для решения системы Крамера необходимо вычислить значения определителей |A|, |Ax| и |Ay|.
Затем, используя формулы Крамера, находим значения переменных x и y:
x = |Ax| / |A|
y = |Ay| / |A|
В данном случае, мы получаем значения x = -1 и y = 2, что является верным решением системы уравнений.
Таким образом, решение системы линейных уравнений по формулам Крамера может быть получено с помощью нахождения определителей и использования специальных формул. Это один из методов, который может использоваться для решения систем уравнений с любыми значениями переменных.
